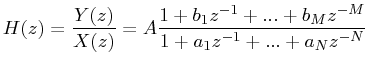Función de transferencia

$\displaystyle H(z) = \frac{Y(z)}{X(z)} = A\frac{1 + b_{1}z^{-1}+ ... + b_{M}z^{-M}}{1 + a_{1}z^{-1}+ ... + a_{N}z^{-N}}$

(8.2)

donde $z^{-1}$ es un retraso unitario y

es la función de transferencia y corresponde a la respuesta de frecuencia del filtro. El teorema fundamental del algebra nos permite reescribir la ecuación 6.2 de la siguiente forma:

$\displaystyle H(z)$	$\displaystyle =$	$\displaystyle \frac{Y(z)}{X(z)}$	(8.3)
	$\displaystyle =$	$\displaystyle A\frac{(1 - q_{1}z^{-1})... (1 - q_{M}z^{-M})}{(1 - p_{1}z^{-1})...(1 - p_{N}z^{-N})}$	(8.4)

donde $q_{i}$ son llamados ceros y $p_{i}$ polos. Los ceros corresponden a valores donde la función de transferencia es cero y los polos a valores donde la función de transferencia tiende a infinito (ver sección 6.1.5).

Dado que la multiplicación en el dominio del tiempo corresponde a una convolución en el dominio de la frecuencia, tomando la transformada

inversa de la ecuación 6.2 se obtiene:

$\displaystyle y(n) = h(n)*x(n) = \sum_{i=0}^{n}h(i)x(n-i)$

(8.5)

donde

se conoce como la respuesta al impulso del filtro, discutida previamente en la sección 1.4.2. Por simple inspección, es fácil comprobar que la ecuación 6.5 se corresponde con la ecuación 6.1. En el caso de filtros no recursivos, o filtros de respuesta al impulso finita, los coeficientes del filtro corresponden directamente a los valores de la respuesta al impulso.

Todo sistema lineal e invariante en el tiempo (LTI) se caracteriza unívocamente por una respuesta al impulso y una respuesa de frecuencia. Cada una de estas respuestas contiene información completa sobre el filtro, pero codificada de una manera diferente. Si una de éstas respuestas es conocida, la otra puede ser obtenida en forma directa a través de la transformada de Fourier. La manera más directa de implementar un filtro digital es mediante la convolución de la señal de entrada con la respuesta al impulso del filtro. Todas los filtros lineales pueden ser implementados de esta manera.